Wer sich schon immer für elektrische Maschinen begeistert hat, und zu deren Modellierung so viel wie möglich wissen will, ist hier richtig. Die Ausgangsbasis sowohl in der Simualtion eier Maschine als auch der Regelung bilden die Gleichungssätze der Maschinen.
Da die elektrischen Maschinen einen Rotor haben, der sich dreht, entsteht in der Maschine eine Koordinatentransformation. Es gibt also im Gegensatz z.b. zu einem Trafo kein natürliches Bezugssystem, in dem die Maschine gerechnet wird.
Selbst wenn man den Ständer im Ständerkoordinatensystem rechnet und damit hofft ohne Koordinatentransformation auszukommen, kommt man spätestens beim Läufer zu der Erkenntnis, dass es ohne nicht geht.
Wenn man also sowieso gezwungen ist, eine Koordinatentransformation durchzuführen, so stellt sich die Frage, welches Bezugsystem als Basis dienen soll. Dies hängt jedoch stark von den persönlichen Vorlieben des Ingenieurs und vom Problem ab.
Die elektrischen Maschinen können auf unterschiedlichste Art gerechnet werden. Dabei unterscheidet man:
Die Beschreibungen erfolgen immer in a/b Koordinaten. Kurze Erklärung: im dreiphasigen System ohne Null sind drei Spannungen und Ströme schlicht überbestimmt. Man könnte zwar auch dreiphasig rechnen, müsste aber ständig aufpassen, dass die dritte Phase wirklich die negative Summe der beiden ersten Phase ist. Also macht man es sich einfach und baut aus einem um 120Grad verschobenen 3-phasigen System ein 2-phasiges mit 90Grad.
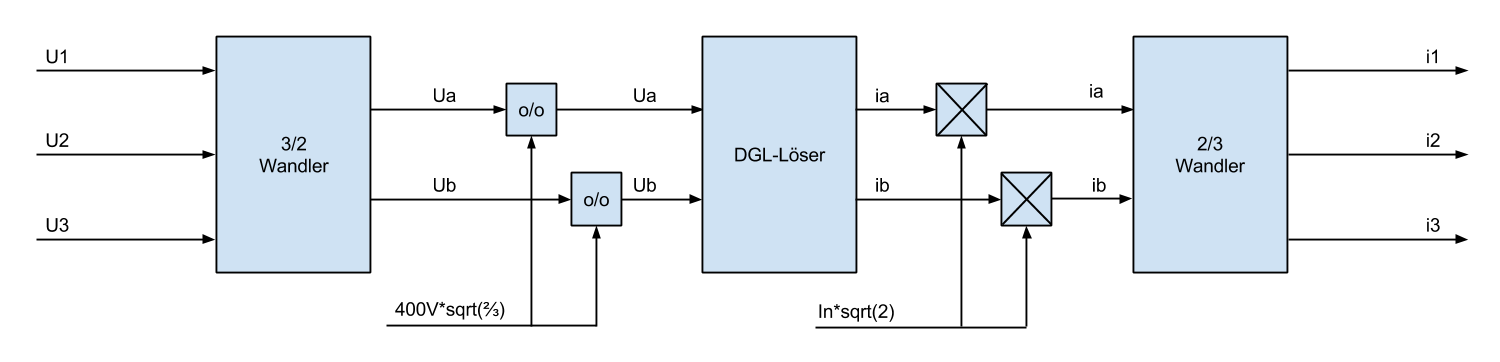
Um auf die relevanten 3-phasigen System zu kommen, kann noch mit einer 3/2 - 2/3 Transformation gearbeitet werden. Die Netzspannungen werden dann erst 3/2 transformiert, durch die Scheitelwerte der Nennspannungen geteilt, dann werden die Maschinengleichungen gerechnet, am Ende werden die Ströme (des DGL-Lösers) wieder mit den Scheitelwerten der Nennströme multipliziert und wieder 2/3 zurücktransformiert.
Eigentlich ganz einfach, oder?
