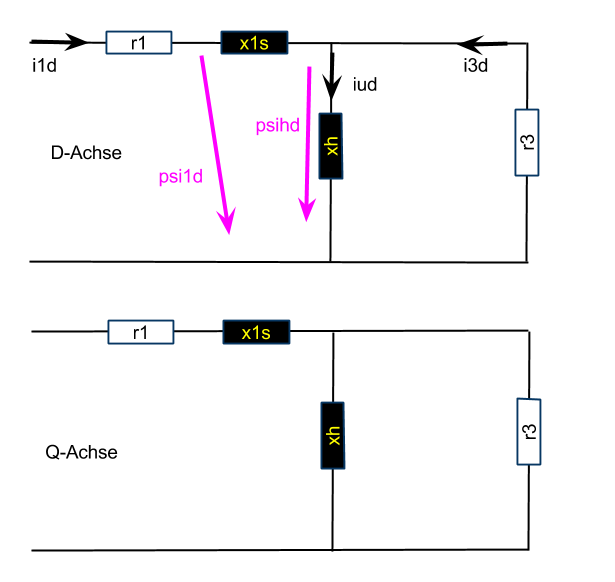
Alle Aussagen zum Ersatzschaltbild selber bleiben gültig. Dies betrifft auch die Umrechnung der Ersatzelemente (ASM: pu, mech-rotor-orientiert, invGam-ESB).
In der klassischen Feldorientierung liegt die Orientierung immer in der D-Achse. Damit liegt die EMK aber in der Q-Achse. In der klassischen Elektrotechnik führt das aber zu einigen Verwirrungen, da hier die Spannung in der D-Achse (also der real-Achse) liegt.
Aber auch die Feldorientierung kann man so machen, dass die EMK in der D-Achse liegt. Hierzu schiebt man die Orientierung also nach \( {\Psi}h_q \), genauer gesagt, da die positive EMK in der D-Achse liegen soll, muss auf \( -{\Psi}h_q \) orientiert werden.
\( {\Psi}h_d \) ist Null.
Die Bezugsdrehzahl des Orientierungssystems ist weiterhin die Ständerfrequenz.
Dieses Ersatzschaltbild mit der Orientierung auf \( {\Psi}h_q \) und sollte (um die älteren Regelungstechniker nicht zu verwirren) nicht für Antriebsregelung verwendet werden.

Die Gleichungen arbeiten alle "pu". Typische Werte:
Die Orientierung des Modells ist neg-q-hauptfeldorientiert.
Die Frequenz ist die Frequenz des Orrientierungssystems, die Ständerfrequenz \( \omega_s \).
Die erste Läufergleichung enthält kein Differential. Diese wird hergenommen, um den Schlupf zu berechnen. Damit lässt sich dann bei bekannter Drehzahl die Ständerfrequenz berechnen.
Ständerfluss:
Auch hier wird es in D-Richtung etwas einfacher, da der Fluss in D-Richtung wegfällt:
Hauptfluss:
Der D-Anteil fehlt wieder:
Wenn es keinen Hauptfluss in D-Richtung gibt, dann gibt es auch keinen Magnetisierungsstrom in D-Richtung.
================================================================
Für alle die das Rumrechnen mit Flüssen überdrüssig sind, kann man eine Asynchronmaschine auch ohne Flüsse rechnen. Das geht zwar prinzipiell mit jedem ASM-Modell, macht aber in dieser Orientierung mehr Freude.
Ausgangspunkt ist der Hauptfluss in Q-Richtung:
und die Stromsummen:
Diese Formeln werden jetzt in die Ständerflussgleichungen eingesetzt:
Die Läufergleichungen können ebenfalls eingesetzt werden:
Die Ständergleichungen werden jetzt allerdings etwas schwieriger:
Das Moment lässt sich auch ausrechnen.
Damit ist die ASM mit 5 Gleichungen beschrieben :-) .
================================================================
Das Drehoment ist: M = Im{psi*conj(I)}
Auch hierbei gilt: Kein Feld in D-Richtung macht die Formel entschieden einfacher:
Der Drehwinkel ist der Orientierungswinkel, auf den die Achsen D und Q bezogen sind
Der Gleichungssatz wurde mit Javascript implementiert.
Der Ausgangspunkt bildet hier ein Unterprogramm, dem eine Struktur mit den von Zeitschritt zu Zeitschritt zu übertragenden Zustandsgrößen, also den Strömen und den Flüssen.
Die Netzspannung und Netzströme in Ständerkoordinaten:Die Ströme in Feldkoordinaten: Die Ströme zeigen am Enfang ein Kurzes einschwingen. Der Magentisierungsstrom bleibt während der ganzen Zeit konstant.
Die Spannungen und Flüsse in Feldkoordinaten: Die Orientierung des Modells erfolgt auf den Hautpfluss. Da der Hauptfluss aber die Ständerfrequenz hat, liegen jetzt alle internen Größen in Gleichgrößen vor. Dies hat den sehr großen Vorteil, das ein normaler PI-Regler jetzt ausreicht, um alles zu regeln.
Die Ströme in Rotorkoordinaten: Sowohl für die Ständer- als auch für die Läuferströme gilt: da das Bezugssystem der Hautpfluss ist, gibt es nur elektrische Gleichgrößen.
Leistungen: Die Leistungen sind sehr übersichtlich. Die Klemmenleistung ist im motrischen Betrieb natürlich höher als die mechanische Leistung. Der Wert der Blindleistung ist das Inverse der bezogenene Hauptinduktivität. Trotz aller Orientierereien: die Blindleistung und die Wirkleistung bleiben im Vergleich mit den Modellen in D-Orientierung gleich.