ASM, invGam-Ersatzschaltbild, feldorientiert (Hauptfluss-d-Richtung), in pu

Allgemeines

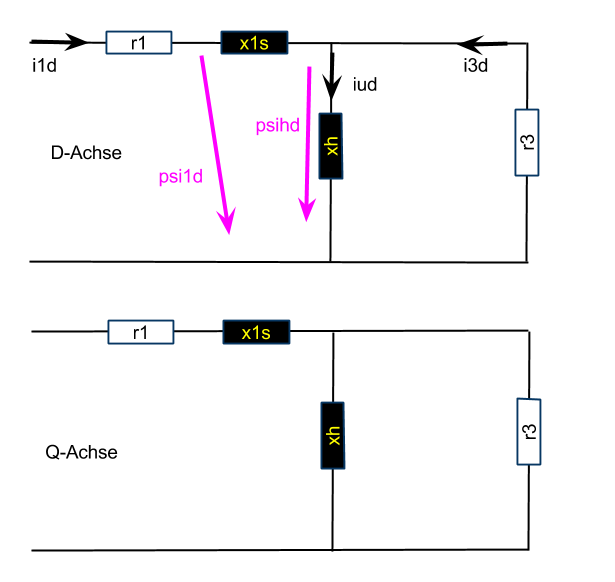
Alle Aussagen zum Ersatzschaltbild selber bleiben gültig. Dies betrifft auch die Umrechnung der Ersatzelemente (ASM: pu, mech-rotor-orientiert, invGam-ESB).

Die Neuerung ist, dass die Orientierung jetzt im Hauptfluss \( {\Psi}h_d \) liegt. Damit ist der Hauptfluss in q-Richtung \( {\Psi}h_q \) aber Null. Ebenso sind die Ableitungen des Hauptflusses in q-Richtung Null.

Zusätzlich gibt es jetzt aber eine Drehzahldifferenz zwischen dem Orientierungspunkt und dem Rotor. Damit werden im Rotor aber auch Feldanteile mit der Schlupffrequenz (Wir erinnern uns: Die Frequenzdifferenz zwischen der Ständerfrequenz und der mechanischen Rotorfrequenz) erzeugt.

Die Orientierung auf den Hauptfluss ändert auch die Bezugsdrehzahl des Orientierungssystems. Jetzt ist diese Orientierungsdrehzahl die Ständerfrequenz.

Dieses Ersatzschaltbild mit der Orientierung auf \( {\Psi}h_d \) ist das klassische Ersatzschaltbild der feldorientierten Regelung

Dafür gibt es auch sehr gute Gründe. Die Orientierung sollte immer auf eine möglichst große Energiemenge erfolgen. Dadurch ist sichergestellt, dass sich ebendiese Orientierung nicht so schnell ändert. Zusätzlich kommt zur Hauptfeldorientierung im invers-gamma Erstazschaltbild hinzu, daß der Hauptfluss elektrich durch den Kurzschlussläufer kurzgeschlossen wird. Da der Fluss aber das Integral einer Spannung ist, und die Spannung im Kurzschlussläufer sehr klein ist, ändert sich der Fluss nur sehr wenig. Dies ermöglicht eine sehr ruhige Orientierung/Regelung.

Formelsatz

Die Gleichungen arbeiten alle "pu". Typische Werte:

• r1 (Ständerwiderstand) : 0.01 … 0.05
• xs1 (Summenstreuung) : 0.03 … 0.15
• xh (Hauptinduktivität) : 2 .. 3
• r3 (Läuferwiderstand) : 0.02 … 0.1

Die Orientierung des Modells ist d-hauptfeldorientiert.

Ständergleichungen (wie T-ESB):

Die Frequenz ist die Frequenz des Orientierungssystems, die Ständerfrequenz \( \omega_s \).

• \( U1_d = r1 \cdot i1_d + \frac{ d{\Psi}1_d }{\omega_n \cdot dt} - \omega_s \cdot {\Psi}1_q \)
• \( U1_q = r1 \cdot i1_q + \frac{ d{\Psi}1_q }{\omega_n \cdot dt} + \omega_s \cdot {\Psi}1_d \)

Läufergleichungen:

da es sich um einen Kurschlussläufer handelt, sind die Spannungen 0. Zusätzlich kommt hier zu der einfachen Ableitung noch die Orientierungsfrequenzdifferenz hinzu, dem Schlupf ss.

• \( U_d = \frac{ d{\Psi}h_d }{\omega_n \cdot dt} - ss \cdot {\Psi}h_q \)
• \( U_q = \frac{ d{\Psi}h_q }{\omega_n \cdot dt} + ss \cdot {\Psi}h_d \)

Da der Hauptfluss in Q-Richtung aber Null ist ebenso wie dessen Ableitungen, vereinfachen sich die Formel stark.

ACHTUNG: Da dieser Formelsatz auf den Hautfluss in D-Richtung orientiert, muss auch sichergestellt werden, dass immer etwas zu orientieren da ist. Bei einer Integration muss man also darauf achten, dass der Fluss in D-Richtung weder Null noch kleiner 0 wird!

Die zweite Läufergleichung enthält kein Differential. Diese wird hergenommen, um den Schlupf zu berechnen. Damit lässt sich dann bei bekannter Drehzahl die Ständerfrequenz berechnen.

• \( 0 = r3 \cdot i3_d + \frac{ d{\Psi}h_d }{\omega_n \cdot dt} \)
• \( 0 = r3 \cdot i3_q \ \ \ \ \ \ \ \ \ \ \ \ \ + ss \cdot {\Psi}h_d \)

Flussgleichungen:

Ständerfluss

Auch hier wird es in Q-Richtung etwas einfacher, da der Fluss in Q-Richtung wegfällt:

• \( {\Psi}1_d = x{\sigma}1 \cdot i1_d + {\Psi}h_d \)
• \( {\Psi}1_q = x{\sigma}1 \cdot i1_q \)

Hauptfluss

Der Q-Anteil fehlt wieder:

• \( {\Psi}h_d = xh \cdot i{\mu}_d \)

Stromsummen:

Wenn es keinen Hauptfluss in Q-Richtung gibt, dann gibt es auch keinen Magnetisierungsstrom in Q-Richtung.

• \( i1_d + i3_d = i{\mu}_d \)
• \( i1_q + i3_q = 0 \)

Drehmoment:

Das Drehoment ist: M = Im{psi*conj(I)}

Auch hierbei gilt: Kein Feld in Q-Richtung macht die Formel entschieden einfacher:

• \( M_{el} = {\Psi}h_d \cdot i1_q \)

Drehwinkel:

Der Drehwinkel ist der Orientierungswinkel, auf den die Achsen D und Q bezogen sind

• \( \omega_s = n + ss \)
• \( \frac{d\rho}{\omega_n \cdot dt} = \omega_s \)

Drehzahl:

• \( \frac{dn}{dt} = \frac{M_{el}-M_{Last}}{ {\tau}_J} \)

Realisierung in einer Programmiersprache

Der Gleichungssatz wurde mit Javascript implementiert.

Der Ausgangspunkt bildet hier ein Unterprogramm, dem eine Struktur mit den von Zeitschritt zu Zeitschritt zu übertragenden Zustandsgrößen, also den Strömen und den Flüssen.