SYM, T-Ersatzschaltbild, dq-mech-rotororientiert, in pu

ACHTUNG: diese Seite verlangt einiges von der Javascript-Engine. Ich empfehle hier (ausnahmsweise) den Chromium.

Allgemeines

Die Synchronmaschine wird in

• Vollpolmaschine und
• Schenkelpolmaschine

Aufgrund der unterschiedlichen Werte für D- und Q-Achse, fällt eine andere, als die mechanische Rotororientierung, schwer.

Die Synchronmaschine wird mechanisch in D- und Q-Achse unterteilt. Dabei bildet die D-Achse die Achse, in der sich die Erregerwicklung befindet. Die Erregerwicklung liegt nur in D-Achse. Das Hauptfeld befindet sich im lastlosen Zustand ebenfalls in der D-Achse. Wenn die Maschine allerdings Drehmoment erzeugt, dann wandert das Hauptfeld aus der D-Achse raus, Richtung Q-Achse.

Bei einer Schenkelpolpaschine hat der Dämpfer in der Q-Achse einen geringeren Widerstand als in der D-Achse, da ja zusätzlich noch die Erregerwicklung in den Anker eingebracht werden muss.

Insgesamt ist der Dämpfer einer Synchronnmaschine aber wesentlich schwächer ausgeprägt als der Dämpfer(der Kurzschlusskäfig :-) ) einer Asynchronmaschine. Ein Dämpferstrom fliest nur bei Arbeitspunktänderungen. Zu diesen zählen auch Oberschwingungen. In der theoretischen Betrachtung ist der Dämpfer im statischen Arbeitspunkt stromlos.

Mit der Dämpferstreuung verhält es sich ähnlich. Da der Dämpfer im Bereich der D-Achse schwächer ist, ist auch die Streuinduktivität höher.

Der Widerstand (in bezogenenen Größen) der Erregerwicklung ist wesentlich kleiner als der Widerstand der Ständerwicklung. Hierbei spielt vor alle der geringere Durchmesser der Läuferwicklung verglichen mit der Ständerwicklung eine Rolle. Die Erregerwicklung wird ständig mit Strom durchflossen und ist damit für den Gesamtwirkungsgrad mitverantwortlich.

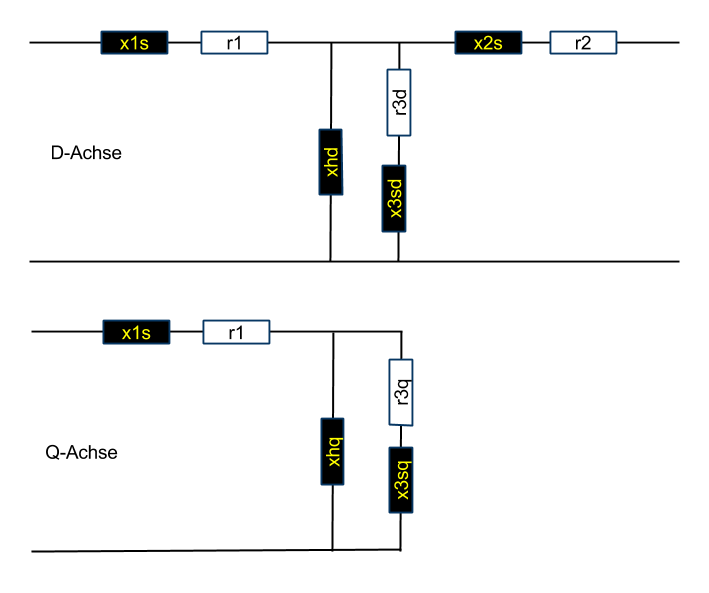
Formelsatz

Die Gleichungen arbeiten alle "pu". Typische Werte:

• r1 (Ständerwiderstand) : 0.005 … 0.05
• xs1 (Ständerstreuung) : 0.03 … 0.15
• xhd (Hauptinduktivität-D) : 1 .. 2
• xhq (Hauptinduktivität-Q) : 0. .. 1
• r2d (Erregerwiderstand-D) : 0.01 … 0.03
• xs2d (Erregerstreuung-D) : 0.1 … 0.2
• r3d (Dämpferwiderstand-D) : 0.1 … 0.4
• r3q (Dämpferwiderstand-Q) : 0.1 … 0.2
• xs3d (Dämpferstreuung-D) : 0.2 … 0.8
• xs3q (Dämpferstreuung-Q) : 0.1 … 0.2

Die Orientierung des Modells ist mechanisch-rotororientiert.

Ständergleichungen:

• \( U1_d = r1 \cdot i1_d + \frac{ d{\Psi}1_d }{\omega_n \cdot dt} - n \cdot {\Psi}1_q \)
• \( U1_q = r1 \cdot i1_q + \frac{ d{\Psi}1_q }{\omega_n \cdot dt} + n \cdot {\Psi}1_d \)

Läufergleichungen:

Hier fangen wir am besten beim Dämpfer an. Die Gleichungen sind hier identisch zu Asynchronmaschine.

• \( 0 = r3_d \cdot i3_d + \frac{ d{\Psi}3_d }{\omega_n \cdot dt} \)
• \( 0 = r3_d \cdot i3_q + \frac{ d{\Psi}3_q }{\omega_n \cdot dt} \)

Die zweite Gleichung beschreibt einfach die Erregung. Da der Erregerwicklung nur in der D-Achse definiert sind, sind die Gleichungsteile der Q-Achse 0. Eine etwaige Verkopplung des Erregerflusses mit dem Dämpferfluss gibt das Ersatzschaltbild nicht her.

• \( U2_d = r2_d \cdot i2_d + \frac{ d{\Psi}2_d }{\omega_n \cdot dt} \)
• \( 0 = 0 \)

Flussgleichungen:

Ständerfluss

• \( {\Psi}1_d = x{\sigma}1 \cdot i1_d + {\Psi}h_d \)
• \( {\Psi}1_q = x{\sigma}1 \cdot i1_q + {\Psi}h_q \)

Die Flussverkettung im Läuferfluss wird jetzt deutlich. Auch der Erregerfluss geht in die Läufergleichungen ein.

• \( {\Psi}2_d = x{\sigma}2 \cdot i2_d + {\Psi}h_d \)
• \( {\Psi}3_d = x{\sigma}3 \cdot i3_d + {\Psi}h_d \)
• \( {\Psi}3_q = x{\sigma}3 \cdot i3_q + {\Psi}h_q \)

Hauptfluss

• \( {\Psi}h_d = xh \cdot i{\mu}_d \)
• \( {\Psi}h_q = xh \cdot i{\mu}_q \)

Stromsummen:

• \( i1_d + i2_d + i3_d = i{\mu}_d \)
• \( i1_q + \ \ \ \ \ \ \ \ \ \ \ i3_q = i{\mu}_q \)

Drehmoment:

Das Drehoment ist: M = Im{psi*conj(I)}

• \( M_{el} = {\Psi}h_d \cdot i1_q - {\Psi}h_q \cdot i1_d \)

Drehwinkel:

Der Drehwinkel ist der Orientierungswinkel, auf den die Achsen D und Q bezogen sind

• \( \frac{d\rho}{\omega_n \cdot dt} = n \)

Drehzahl:

• \( \frac{dn}{dt} = \frac{M_{el}-M_{Last}}{ {\tau}_J} \)

Realisierung in einer Programmiersprache

Der Gleichungssatz wurde mit Javascript implementiert.

Der Ausgangspunkt bildet hier ein Unterprogramm, dem eine Struktur mit den von Zeitschritt zu Zeitschritt zu übertragenden Zustandsgrößen, also den Strömen und den Flüssen.

Insgesamt muss man it der Simulation aber sehr vorsichtig sein. Der starke induktive Knoten in der D-Achse fordert seinen Tribut in kleinen Zeitschritten. Insbesondere der hier verwendete explizite Euler kommt an seine Grenzen.