ASM, T-Ersatzschaltbild, psih-D-feldorientiert, in pu
Allgemeines
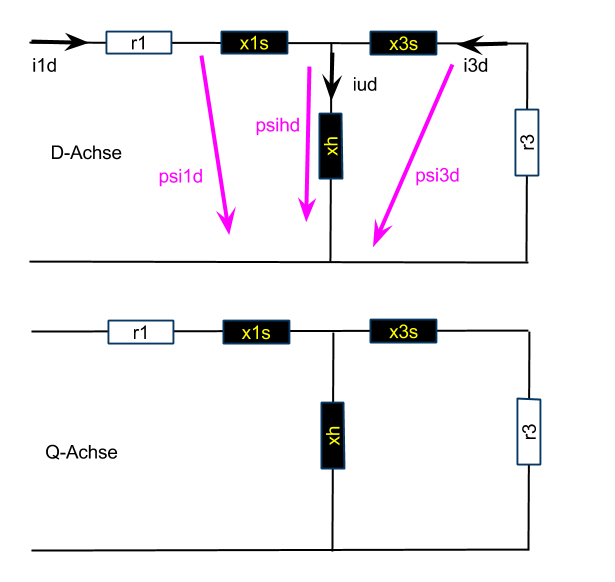
Alles Wesentliche zum Ersatzschaltbild wurde schon beim Ersatzschaltbild Gamma-mechRot gesagt.
Die Orientierung erfolgt auf den Hauptfluss. Das Modell wird hierdiurch etwas komplizierter. Dieses Modell sollte man nur für Spezialfälle nehmen.
Modelliering in Simplorer VHDL-AMS
Formelsatz
Die Gleichungen arbeiten alle "pu". Typische Werte:
- r1 (Ständerwiderstand) : 0.01 … 0.05
- xs1 (Ständerstreuung) : 0.03 … 0.15
- xh (Hauptinduktivität) : 2 .. 3
- r3 (Läuferwiderstand) : 0.02 … 0.1
- xs3 (Läuferstreuung) : 0.03 … 0.15
Das Modell orientiert auf den Hauptfluss in D-Richtung. Der Fluss in Q-Richtng ist also Null. Damit ist auch der Magnetisierungsstrom in Q-Richtung Null.
Ständergleichungen in [pu] :
Beide Ständergleichungen haben ein Differential. Die Ständerfrequenz \( \omega_s \) kommt dazu.
- (1) \( U1_d = r1 \cdot i1_d + \frac{ d{\Psi}1_d }{\omega_n \cdot dt} - \omega_s \cdot {\Psi}1_q \)
- (2) \( U1_q = r1 \cdot i1_q + \frac{ d{\Psi}1_q }{\omega_n \cdot dt} + \omega_s \cdot {\Psi}1_d \)
Läufergleichungen in [pu] :
da es sich um einen Kurschlussläufer handelt, sind die Spannungen 0. Es kommt noch die Schlupffrequenz \( ss \) dazu.
- (3) \( 0 = r3 \cdot i3_d + \frac{ d{\Psi}3_d }{\omega_n \cdot dt} - ss \cdot {\Psi}3_q \)
- (4) \( 0 = r3 \cdot i3_q + \frac{ d{\Psi}3_q }{\omega_n \cdot dt} + ss \cdot {\Psi}3_d \)
Flussgleichungen in [pu] :
Ständerfluss
- (5) \( {\Psi}1_d = x{\sigma}1 \cdot i1_d + {\Psi}h_d \)
- (6) \( {\Psi}1_q = x{\sigma}1 \cdot i1_q \)
Hauptfluss
Läuferfluss
- (8) \( {\Psi}3_d = x{\sigma}3 \cdot i3_d + {\Psi}h_d \)
- (9) \( {\Psi}3_q = x{\sigma}3 \cdot i3_q \)
Stromsummen in [pu] :
Der Magnetisierungstrom in Q-Richtung fällt weg.
- (10) \( i1_d + i3_d = i{\mu}_d \)
- (11) \( i1_q + i3_q = 0 \)
Frequenzen in [pu] :
- (12) \( \omega_s = n + ss \)
Anzahl der elektrischen Gleichungen:
Die Anzahl der Gleichungen muss der Anzahl der Unbekannten entsprechen.
- 5x Fluss: \( {\Psi}1_d , {\Psi}1_q , {\Psi}h_d , {\Psi}3_d , {\Psi}3_q \)
- 5x Strom: \( i1_d , i1_q , i{\mu}_d , i3_d , i3_q \)
- 2x Frequenz: \( ss , \omega_s \)
- 12x Gleichungen (passt)
Drehmoment:
Das Drehoment ist: M = Im{psi*conj(I)}. (\( M_{el} = {\Psi}h_d \cdot i1_q - {\Psi}h_q \cdot i1_d \))
Der Q-Anteil vom Fluss ist 0, damit fliegt der raus.
- \( M_{el} = {\Psi}h_d \cdot i1_q \)
Drehwinkel:
Der Drehwinkel ist der Orientierungswinkel, auf den die Achsen D und Q bezogen sind
- \( \frac{d\rho}{\omega_n \cdot dt} = \omega_s \)
Drehzahl:
- \( \frac{dn}{dt} = \frac{M_{el}-M_{Last}}{ {\tau}_J} \)
Realisierung in einer Programmiersprache
-> das Umstellen das Formelsatzes ist etwas schwierig :-).
Hier muss wahrscheinlich mit einem
Gleichungslöser
gearbeitet werden.
Um einen Gleichunglöser zu nutzen müssen alle Gleichungen auf einer Seite eine Null haben. Das sollte machbar sein :-)
Die Netzspannung in Ständerkoordinaten:
Die Ströme in Ständerkoordinaten:
Die Ströme zeigen ein kurzes Einschwingen. Da der Motor mit Nennlast betrieben wird,
sind die Strangströme (i1_ab) praktisch in Phase zur Netzspannung, da der Magnetisierungsstrom
nicht weiter auffällt.
In Feldkoordinaten:
Die Spannungen und Flüsse in Feldkoordinaten:
Da wir auf den Hauptfluss orintieren, sollten alle Q-Kompoenten der Flüsse nahe 0 sein.
Die Spannungen liegen alle in der Q-Achse.

