ASM, Gam-Ersatzschaltbild, psih-D-feldorientiert, in pu

Allgemeines

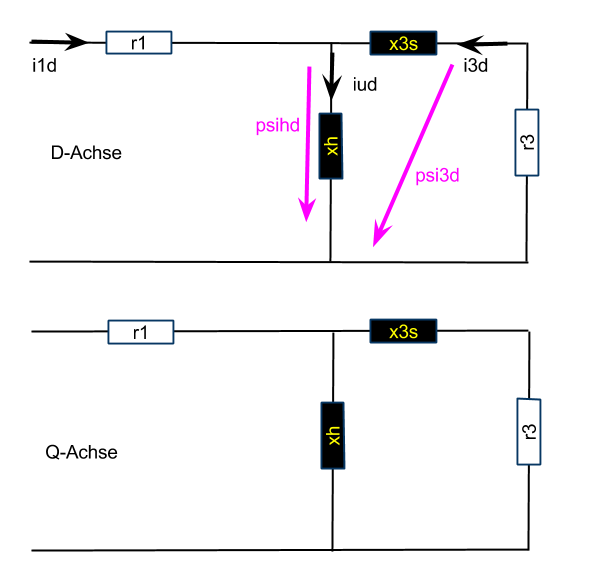
Alles Wesentliche zum Ersatzschaltbild wurde schon beim Ersatzschaltbild Gamma-mechRot gesagt.

Die Orientierung auf der Ständerfluss hat bei neueren Regelverfahren Einzug gehalten. Als großer Vorteil wird hier der direkte Zugriff auf den Ständerfluss gesehen, der die Regelung dynamischer macht. Ebenso fällt die Orientieungsberechnung leichter, da von der Klemmenspannung nur die ohmschen Spannungsabfälle abgezogen werden müssen danach wird diese Spannung (EMK) einfach nur integriert. Die beim invers-gamma notwendigen komplizierteren Flussmodelle zur Orientierungsberechnung können also entfallen.

Formelsatz

Die Gleichungen arbeiten alle "pu". Typische Werte:

• r1 (Ständerwiderstand) : 0.01 … 0.05
• xs1 (Summenstreuung) : 0.03 … 0.15
• xh (Hauptinduktivität) : 2 .. 3
• r3 (Läuferwiderstand) : 0.02 … 0.1

Das Modell orientiert auf den Hauptfluss in D-Richtung.

Ständergleichungen :

Die Frequenz ist die Frequenz des Orientierungssystems, die Ständerfrequenz \( \omega_s \). Es fallen natürlich die Q-Anteile im Fluss weg.

In der zweiten Ständergleichung findet sich kein Differential. Die Gleichung kann deshalb dazu verwendet werden, die Ständerfrequenz zu berechnen.

• \( U1_d = r1 \cdot i1_d + \frac{ d{\Psi}h_d }{\omega_s \cdot dt} \)
• \( U1_q = r1 \cdot i1_q \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \omega_s \cdot {\Psi}h_d \)

Läufergleichungen:

da es sich um einen Kurschlussläufer handelt, sind die Spannungen 0. Es kommt noch die Schlupffrequnz dazu.

• \( 0 = r3 \cdot i3_d + \frac{ d{\Psi}3_d }{\omega_n \cdot dt} - ss \cdot {\Psi}3_q \)
• \( 0 = r3 \cdot i3_q + \frac{ d{\Psi}3_q }{\omega_n \cdot dt} + ss \cdot {\Psi}3_d \)

Flussgleichungen:

Läuferfluss

• \( {\Psi}3_d = x{\sigma}3 \cdot i3_d + {\Psi}h_d \)
• \( {\Psi}3_q = x{\sigma}3 \cdot i3_q \)

Hauptfluss

Den Hauptfluss gibt es nur in D-Richtung.

• \( {\Psi}h_d = xh \cdot i{\mu}_d \)

Stromsummen:

Der Magnetisierungstrom in Q-Richtung fällt weg.

• \( i1_d + i3_d = i{\mu}_d \)
• \( i1_q + i3_q = 0 \)

Drehmoment:

Das Drehoment ist: M = Im{psi*conj(I)}

• \( M_{el} = {\Psi}h_d \cdot i1_q - {\Psi}h_q \cdot i1_d \)

Drehwinkel:

Der Drehwinkel ist der Orientierungswinkel, auf den die Achsen D und Q bezogen sind

• \( \omega_s = n + ss \)
• \( \frac{d\rho}{\omega_n \cdot dt} = \omega_s \)

Drehzahl:

• \( \frac{dn}{dt} = \frac{M_{el}-M_{Last}}{ {\tau}_J} \)

Realisierung in einer Programmiersprache

Der Gleichungssatz wurde mit Javascript implementiert.

Der Ausgangspunkt bildet hier ein Unterprogramm, dem eine Struktur mit den von Zeitschritt zu Zeitschritt zu übertragenden Zustandsgrößen, also den Strömen und den Flüssen.