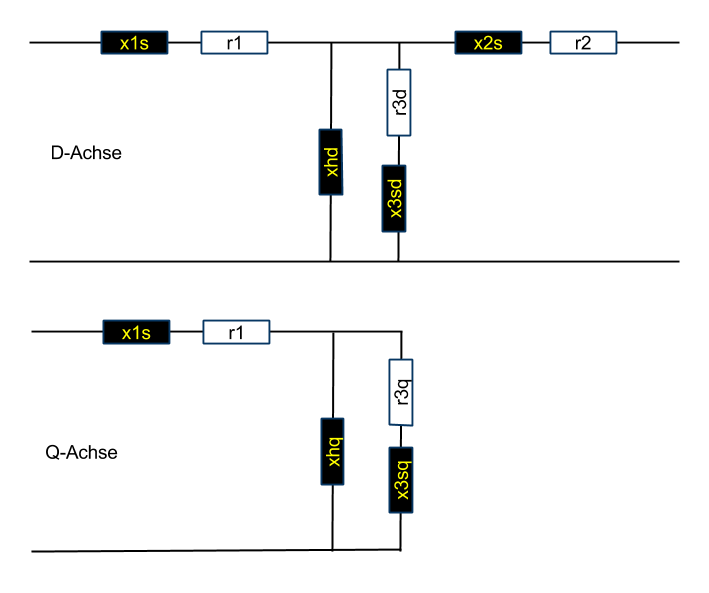
Die Synchronmaschine wird traditionell mit Summenreaktanzen angegeben. Aber das kann man umrechnen.

| ddd3 | ||||
| ddd3 | ||||
| ddd1 | ||||
| ddd2 | dddd | |||
| ddd2 | dddd | |||
| ddd1 | ||||
| Kurzschlusserregerstrom | ddd1 | |||
| Ständerwiderstand | ddd1 | ddd2 | dddd | |
| Ständerstreuung | ddd1 | ddd2 | dddd | |
| Synchronreaktanz | ddd1 | ddd1 | ||
| transiente Synchronreaktanz | ddd1 | |||
| subtransiente Synchronreaktanz | ddd1 | ddd1 | ||
| transiente Zeitkonstante | ddd1 | |||
| subtransiente Zeitkonstante | ddd1 | ddd1 | ||
| Ankerzeitkonstante(DC) | ddd2 | dddd | ||
| Hauptinduktivität | ddd2 | dddd | ddd2 | dddd |
| ddd2 | dddd | ddd2 | dddd | |
| Erregerindutivität | ddd2 | dddd | ddd2 | dddd |
| Erregerwiderstand | ddd2 | dddd | ddd2 | dddd |
| Dämpferstreuung | ddd2 | dddd | ddd2 | dddd |
| ddd2 | dddd | ddd2 | dddd | |
| Dämpferwiderstand | ddd2 | dddd | ddd2 | dddd |
| ddd2 | dddd | ddd2 | dddd | |
| Stromuebersetzung | ddd2 | dddd | ||
| Spannunguebersetzung | ddd2 | dddd | ||
| Kurzschlussstrom | ddd2 | dddd | ||
| Kurzschlussstrom peak | ddd2 | dddd |