Lösung für Beispiel 2
Mit Matlab
Die nachfolgenden Grafiken geben eine Übersicht über die einzelnen Integrationsverfahren für Beispiel 2.
Lösung mit dem impliziten Euler:
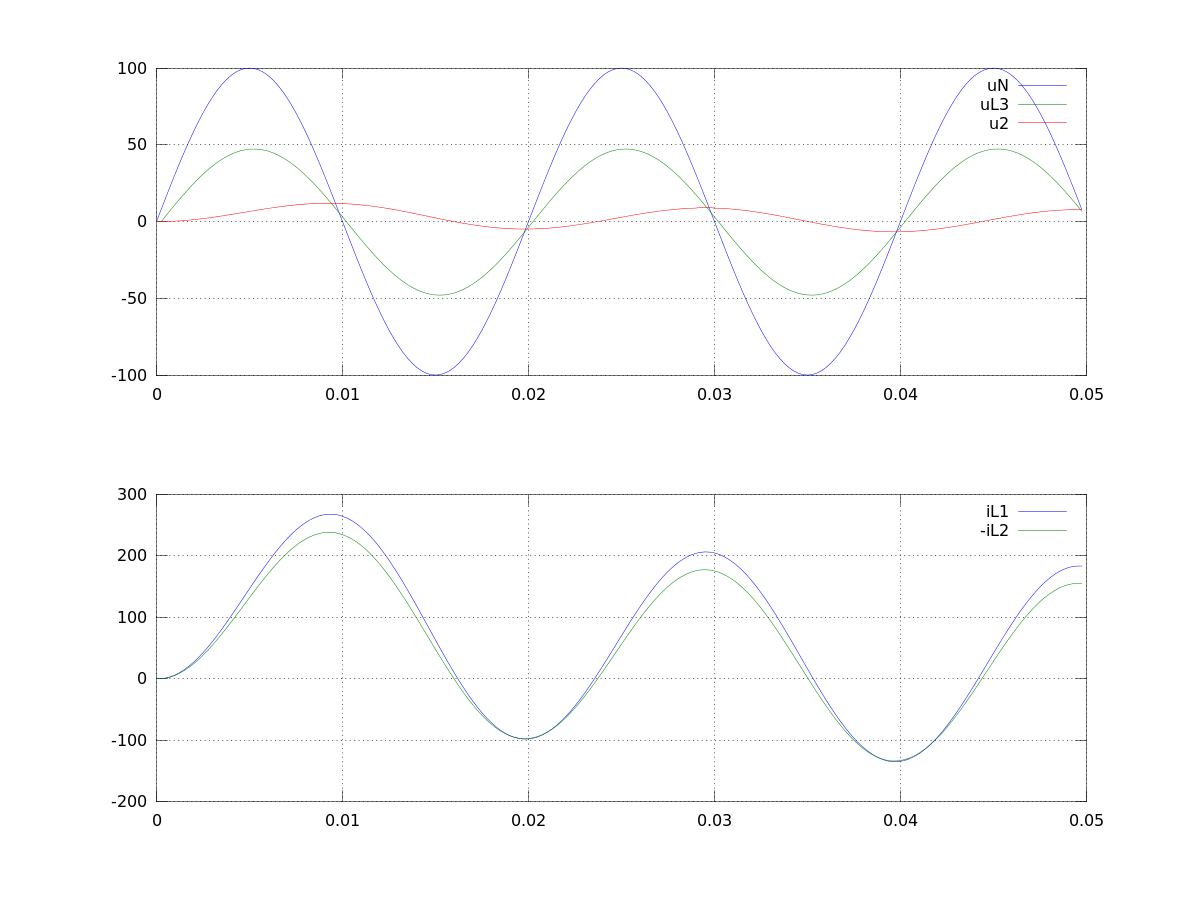
Lösung mit dem Trapezverfahren:
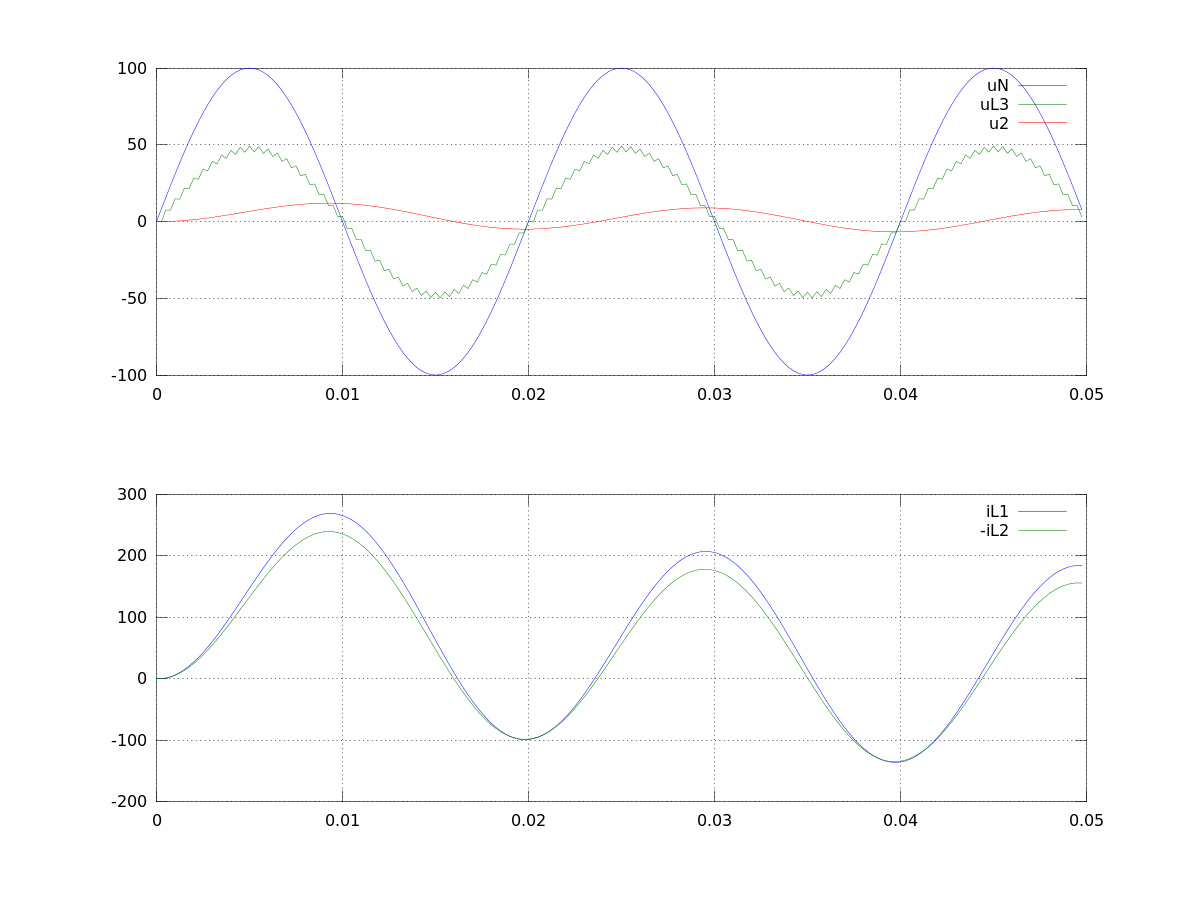
Matlab script zur Lösung 2
clear all
L1 = 1e-3;
L2 = 1e-3;
L3 = 10e-3;
R1 = 50e-3;
R2 = 50e-3;
A1 = [0 , 0 , 0 , 0 , 0 , 0
; 0 , 0 , 0 , 0 , 0 , 0
; 0 , 0 , 0 , 0 , 0 , 0
; 0 , 0 , 0 ,L1 , 0 , 0
; 0 , 0 , 0 , 0 ,L2 , 0
; 0 , 0 , 0 , 0 , 0 ,L3]
B1 = [-1/R1 , 0 , 1/R1 , 1 , 0 , 0
; 0 , -1/R2 , 0 , 0 , -1 , 0
; 1/R1 , 0 , -1/R1 , 0 , 1 , -1
; 1 , 0 , 0 , 0 , 0 , 0
; 0 , -1 , 1 , 0 , 0 , 0
; 0 , 0 , -1 , 0 , 0 , 0 ];
for z = 1:2
fn = 50;
dt = 0.25e-3;
x0 = [0 ; 0 ; 0 ; 0 ; 0 ; 0];
t = 0;
for k = 1:200
C1 = [0 ; 0 ; 0 ; 100 * sin(2 * pi * fn * t) ; 0 ; 0];
if z==1
% impliziter Euler
x1 = inv(A1 + dt * B1) * (A1 * x0 + dt * C1 );
else
% trapez
x1 = inv(A1 + dt * B1 / 2) * ( (A1 - dt * B1 / 2) * x0 + dt * C1);
end
% zuweisen der Ergebnisse aus dem alten Zeitschritt
tx(k) = t;
uN(k) = C1(4);
u2(k) = x0(2);
uL3(k) = x0(3);
iL1(k) = x0(4);
iL2(k) = x0(5);
iL3(k) = x0(6);
% umlegen der Zeitschritte
x0 = x1;
t = t + dt;
end
figure(z)
subplot(2,1,1) , plot( tx,uN , tx,uL3 , tx,u2 ) , grid on , legend('uN','uL3','u2')
subplot(2,1,2) , plot( tx,iL1 , tx,-iL2 ) , grid on , legend('iL1','-iL2')
print(['matrix_' num2str(z) '_verg.png'],'-dpng')
end