Differentialgleichungen

Um eine Differentialgleichung zu lösen, gibt es mehrere Ansätze. Die “manuellen” Ansätze versuchen das Problem geschlossen zu lösen. Man versucht hierbei eine Stammfunktion zu finden, die der Differentialgleichung genügt. Man kann die Differentialgleichungen allerdings auch in kleinen Schritten numerisch lösen. Damit wird aus den Differentialgleichungen eine partielle Differentialgleichung. Da es sich um einen sehr kleinen Zeitabschnitt handelt, kann man die Lösung auch mit einem einfachen Polynom abstrahieren. Im einfachsten Fall kann man die Lösung innerhalb des Zeitschrittes linear abstrahieren. Es handelt sich dabei im Normalfall um eine "numerische Zeitschrittsimulation" einer "partiellen Differentialgleichung".

Im Falle der Lösung elektrotechnischer Probleme wird auch heute immer noch gern für die stationäre Lösung auf die "manuelle" Lösung zurückgegriffen. Dies ist allgemein unter dem Namen "komplexe Wechselstromtheorie" bekannt. Hier soll auf diese aber nicht eingegangen werden.

Das Problem der numerischen Integration ist schon sehr alt, so daß man glücklicherweise die Mathematik hierfür nicht selbst entwickeln muss.

Zum Thema:

Um eine Differentialgleichung mit Hilfe der numerischen Mathematik zu lösen, muss die Differentialgleichung (engl.: ODE) in eine bekannte Form überführt werden:

1. als Definition des Differentialquotienten
2. als lineares Differentialgleichungssystem erster Ordnung:

Um eine Differentialgleichung numerisch zu lösen, ist es am einfachsten, die Gleichung im Arbeitspunkt zu linearisieren und dann eine Lösung zu versuchen.

Übersicht über die numerischen Integrationsverfahren

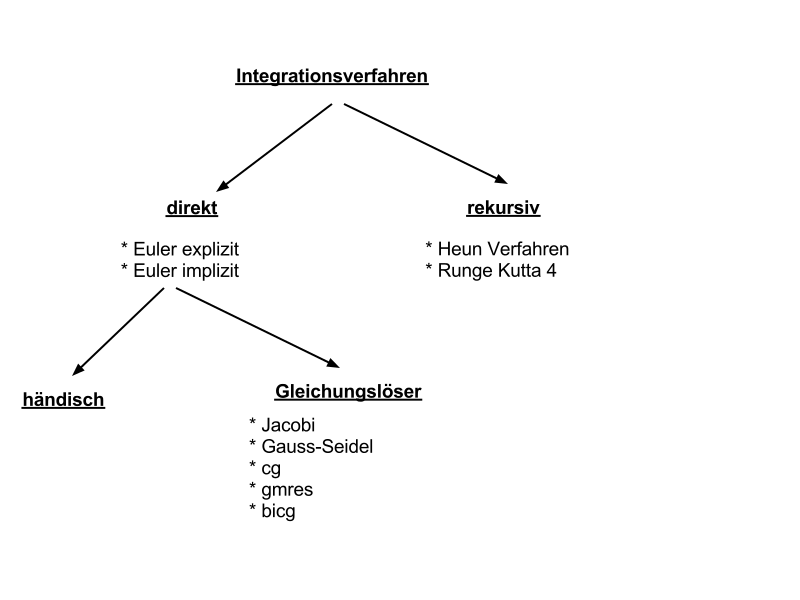
Die numerischen Integrationsverfahren lassen sich in direkte und rekursive Verfahren einteilen. Die direkten Verfahren versuchen sich an einer schnellen Einschrittlösung, wogegen die rekursiven Verfahren sich über (meist mehrere) Iterationen an eine Näherungslösung heranarbeiten. Auf die Gleichungslöser wird später eingegangen.

Nachfolgende Beispiel sollen die Möglichkeiten zum Lösen von Differentialgleichungen zeigen.

1. Als erstes Beispiel wird eine einfache LR-Kombination untersucht. Dabei soll nur der Strom ausgerechnet werden.

   

   Die Maschengleichung liefert dann die folgende Formel: \( \;\; E(t) = L \cdot \frac{di}{dt} + R \cdot i \)

2. Als zweites Beispiel wird ein kurzgeschlossener Trafo untersucht. Hier sollen neben den Strömen auch alle Knotenpotentiale gerechnet werden.

   

   Dazu müssen wir jetzt allerdings etwas tiefer in die Trickkiste greifen, und eine kleine Kontenpotentialanalyse machen. Die Knotenpotentialanalyse geht erstmal von der Stromsumme im Knoten aus:

   1. Knoten: \( \;\; i_{L1} + \frac{U_3-U_1}{R1} = 0 \)
   2. Knoten: \( \;\; -i_{L2} + \frac{0-U_2}{R2} = 0 \)
   3. Knoten: \( \;\; \frac{U_1-U_3}{R1} + i_{L2} - i_{L3}= 0 \)

   Die Differentiale der Induktivitäten müssen getrennt behandelt werden.

   1. Masche L1: \( \;\; U_1 + L_1 \cdot \dot{i_{L1}} = E(t) \)
   2. Masche L2: \( \;\; U_3 + L_2 \cdot \dot{di_{L2}} = U2 \)
   3. Masche L3: \( \;\; L_3 \cdot \dot{di_{L3}} = U3 \)

   Die 6 Gleichungen kann man dann in eine Matrixform bringen.

   $$ \begin{pmatrix} . & . & . & . & . & . \\ . & . & . & . & . & . \\ . & . & . & . & . & . \\ . & . & . & L_1 & . & . \\ . & . & . & . & L_2 & . \\ . & . & . & . & . & L_3 \\ \end{pmatrix} \cdot \begin{pmatrix} \dot{U1} \\ \dot{U2} \\ \dot{U3} \\ \dot{i_{L1}} \\ \dot{i_{L2}} \\ \dot{i_{L3}} \\ \end{pmatrix} + \begin{pmatrix} -\frac{1}{R_1} & . & \frac{1}{R_1} & 1 & . & . \\ . & -\frac{1}{R_2} & . & . & -1 & . \\ \frac{1}{R_1} & . & -\frac{1}{R_1} & . & 1 & -1 \\ 1 & . & . & . & . & . \\ . & -1 & 1 & . & . & . \\ . & . & -1 & . & . & . \\ \end{pmatrix} \begin{pmatrix} U1 \\ U2 \\ U3 \\ i_{L1} \\ i_{L2} \\ i_{L3} \\ \end{pmatrix} = \begin{pmatrix} . \\ . \\ . \\ E(t) \\ . \\ . \\ \end{pmatrix} $$ Diese Matrixschreibweise kann man zur besseren Lesbarkeit abkürzen: \( \;\; A_1 \cdot \dot{x} + B_1 \cdot x = C_1 \)

Weiterlesen

Wer mit den einfachen Lösern nicht weiterkommt, kann es mit der Klasse der impliziten Verfahren versuchen. Hier tut sich das Adams-Moulton-Verfahren als Obermenge hervor ( Mehrschrittverfahren).

Wer es lieber explizit mag, der kommt mit dem Adams-Bashforth-Verfahren weiter (BDF-Verfahren).

Weiter