Lösung für Beispiel 1
Mit Matlab
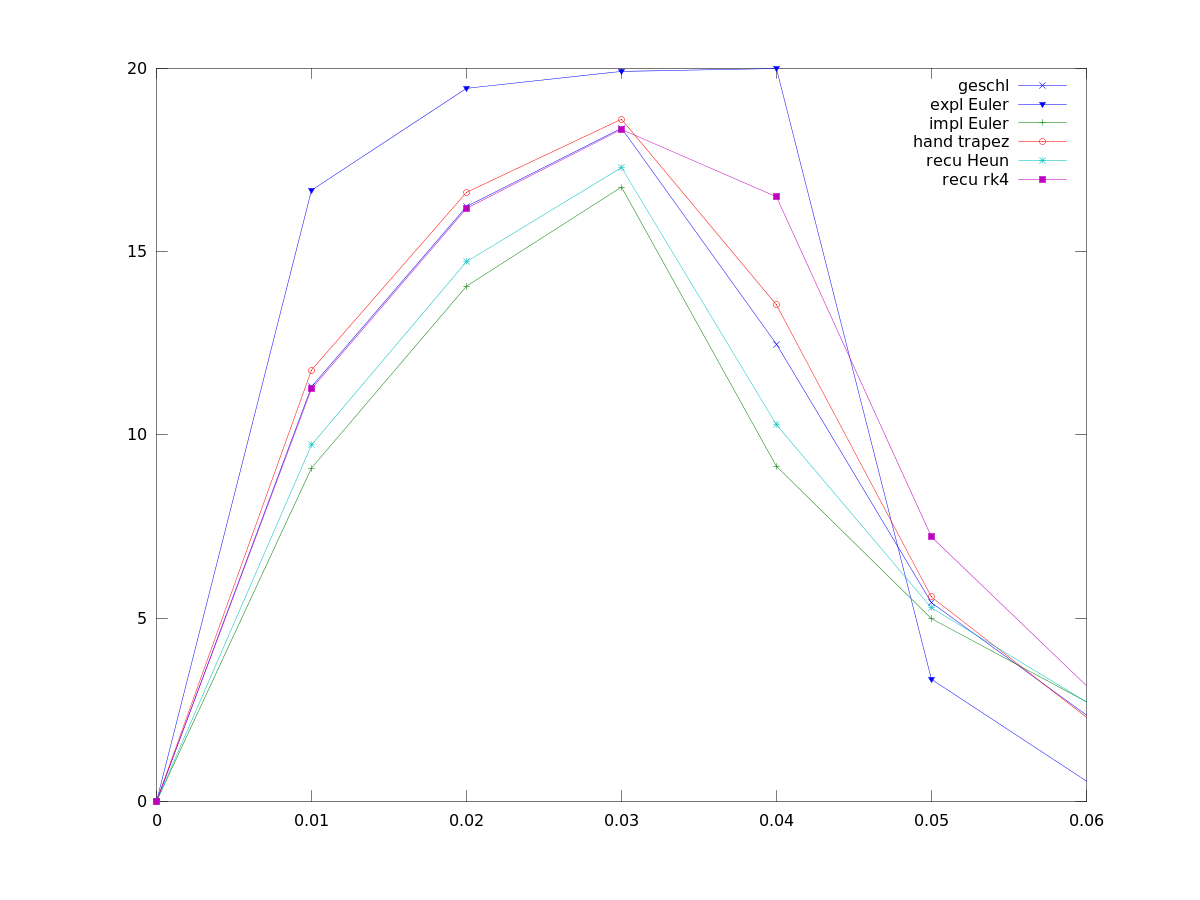
Die nachfolgende Grafik gibt eine Übersicht über die einzelnen Integrationsverfahren für Beispiel 1.
Die Spannung E ist 10V, L=6mH, R=0.5Ohm
Matlab script zur Lösung 1:
clear all
dt = 5 * 2e-3; % Integrationsschrittweite
tend = 70e-3;
L = 6e-3; % Induktivitaet 6mH
R = 0.5; % Widerstand 0.5ohm
t0 = 0;
k = 1;
t(1) = 0;
t1 = 0;
expl_Euler.i1 = 0;
impl_Euler.i1 = 0;
hand_trapez.i1 = 0;
recu_Heun.i1 = 0;
recu_rk4.i1 = 0;
while t1 < tend
% Die Zeit integrieren
t0 = t1;
t1 = t0 + dt;
t12 = t0 + dt / 2;
k = k + 1;
% % Die Variablen ablegen
t(k) = t1;
% Die Spannung
e0 = 10 * (t0 < tend / 2);
e1 = 10 * (t1 < tend / 2);
e12 = 10 * (t12 < tend / 2);
e(k) = e0;
% Integration expliziter Euler
i0 = expl_Euler.i1;
expl_Euler.di = ( e0 - R* i0 ) / L ;
expl_Euler.i1 = i0 + dt * expl_Euler.di;
expl_Euler.i(k) = expl_Euler.i1;
% Integration impliziter Euler
i0 = impl_Euler.i1;
impl_Euler.i1 = ( L* i0 + dt * e1) / (L + dt*R);
impl_Euler.i(k) = impl_Euler.i1;
% Integration hand-Trapez
i0 = hand_trapez.i1;
hand_trapez.i1 = (( e0 -R * i0 + e1 ) * dt + 2 * i0 * L) / (2 * L + dt * R);
hand_trapez.i(k) = hand_trapez.i1;
% Integration Recursion Heun
i0 = recu_Heun.i1;
i1A = i0 + dt * ( e0 - R * i0 ) / L; % expliziter Eulerschritt
i1B = i0 + dt * ( e1 - R * i1A ) / L; % recursiver Schritt
recu_Heun.i1 = (i1A + i1B) / 2; % recursiver Schritt
ecu_Heun.i(k) = recu_Heun.i1;
% Integration Recursion Runge-Kutta-4
i0 = recu_rk4.i1;
di0 = ( e0 - R * i0 ) / L;
i1A = i0 + dt / 2 * di0 ; di1A = ( e12 - R * i1A ) / L;
i1B = i0 + dt / 2 * di1A ; di1B = ( e12 - R * i1B ) / L;
i1C = i0 + dt * di1B ; di1C = ( e1 - R * i1C ) / L;
recu_rk4.i1 = i0 + dt / 6 * (di0 + 2 * di1A + 2 * di1B + di1C);
recu_rk4.i(k) = recu_rk4.i1;
end
% geschl Lösung
tau = L / R;
igeschl1 = 0 .* exp(-t / tau) + 10/R .* (1-exp(-t / tau));
igeschl2 = 10 / R .* (1-exp(-tend / 2 / tau)) * exp(-(t-tend / 2) / tau);
igeschl = igeschl1 .* (t <= tend / 2) + igeschl2 .* (t < tend / 2);
plot(
t, igeschl , '-xb',...
t, expl_Euler.i , '-v',...
t, impl_Euler.i ,'-+', ...
t, hand_trapez.i ,'-o', ...
t, recu_Heun.i ,'-*', ...
t, recu_rk4.i ,'-s')
legend('geschl','expl Euler','impl Euler','hand trapez','recu Heun','recu rk4')
xlim([0 0.06])
print('dgl_verg.png','-dpng')