Der implizite Euler
Der implizite Euler nimmt zur Arbeitspunktbestimmung immer den neuen Arbeitspunkt. Dies ist sehr verwunderlich, da der neue Arbeitspunkt erst durch das Verfahren ausgerechnet werden muss. Dieses generelle Problem muss beim impliziten Euler-Verfahren gelöst werden.
Dieses Verfahren verwendet also einen Arbeitspunkt, der erst durch die Integration entstehen wird. Wer sich jetzt an Münchhausen ( * es ist das Abenteur gemeint, als er sich am eigenen Schopf aus dem Moor zieht ) erinnert fühlt, hat das Problem verstanden.
Das implizite Euler-Verfahren kann man daran erkennen, daß \( x_{k+1} \) auf beiden Seiten der Gleichung zu finden ist.
\[ x_{k+1} = x_k + \Delta t \cdot f(x_{k+1}) \;\; \to \;\; x_{k+1} = i_k + \Delta t \cdot \frac{E(t_k)-R \cdot i_{k+1} }{L} \]
Die Formel muss jetzt noch nach \( i_{k+1} \) umgestellt werden. Dies fällt bei einer Formel dieses Schwierigkeitsgrades noch nicht sehr schwer. Zuerst werden noch ein paar Vereinfachungen getroffen:
\[i0 = i(k) \] \[ i1 = i_k+1 \] \[e0 = E(t_k) \] \[ e1 = E(t_{k+1}) \]
Dadurch ergibt sich als programmiererfreundliche Version:
$$ i1 = \frac{i0 \cdot L+\Delta t \cdot e1}{L+\Delta t \cdot R} $$
Die grafische Lösung erkennt man daran, dass die Lösung tendenziell etwas "nachhängt":
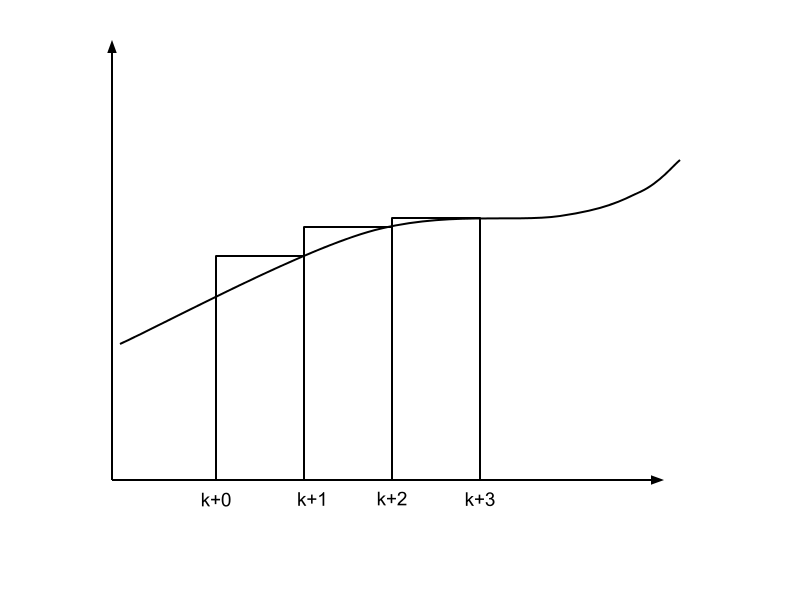
Da in der Gleichung einige Konstanten sind, muss in der numerischen Integration nicht zwingend alles neu gerechnet werden. Insbesondere, wenn sich die Schrittweite nicht ändert, kann der Divisor ( \( L+\Delta t \cdot R \) ) als konstant angenommen werden.
Das zweite Beispiel ist etwas komplizierter. Wir steigen in den Gleichungssatz vom expliziten Euler ein und modifizieren etwas.
Aus dem expliziter Euler:
\[
x1 = x0 + \Delta t \cdot A_1^{-1} \cdot (C_1-B_1 \cdot x0)
\]
wird durch den Ersatz von \( x0 \) durch \( x1 \) der implizite Euler:
\[
x1 = x0 + \Delta t \cdot A_1^{-1} \cdot (C_1-B_1 \cdot x1)
\]
nach ein wenig umstellen wird daraus dann:
\[
x1 = (A_1 + \Delta t \cdot B_1)^{-1} \cdot
(A_1 \cdot x0 + \Delta t \cdot C1)
\]
Hier fällt im Gegensatz zum expliziten Euler auf, daß der zu invertierende Teil aus der mit der Schrittweite bewerteten Summe beider Matrizen besteht. Diese Summe sollte immer invertierbar, da eine Matrix mit einer vollbesetzten Hauptdiagonale meist eine von 0 verschiedene Determinante hat. Als Nachteil bleibt, dass diese Summe auch von \( \Delta t\) abhängt. Damit muss bei einer Lösung mit variabler Schrittweite die Matrixinversion auch praktisch häufig durchgeführt werden.
Die mathematisch sehr stabile Lösung wird durch große Rechenaufwendungen erkauft.