Der explizite Euler
Der explizite Euler ist eines der einfachsten Integrationsverfahren. Das Verfahren besticht durch seine einfache Art der mathematischen Umsetzung.
Bei diesem Verfahren wird der alte Zustand dazu verwendet, den Differenzenquotienten auszurechnen. Dann wird dieser Differenzenquotient dazu verwendet, den neuen Zustand auszurechnen. In der Zeitschrittform wird also eine Gleichung in der folgenden Form benötigt: \[i_{k+1} = i_k + \Delta t \cdot \frac{di}{dt} \]
Dieses Verfahren verwendet zur Berechnung des Differentialqotienten imer den alten Wert. Die Lösung der sieht dann grafisch so aus:
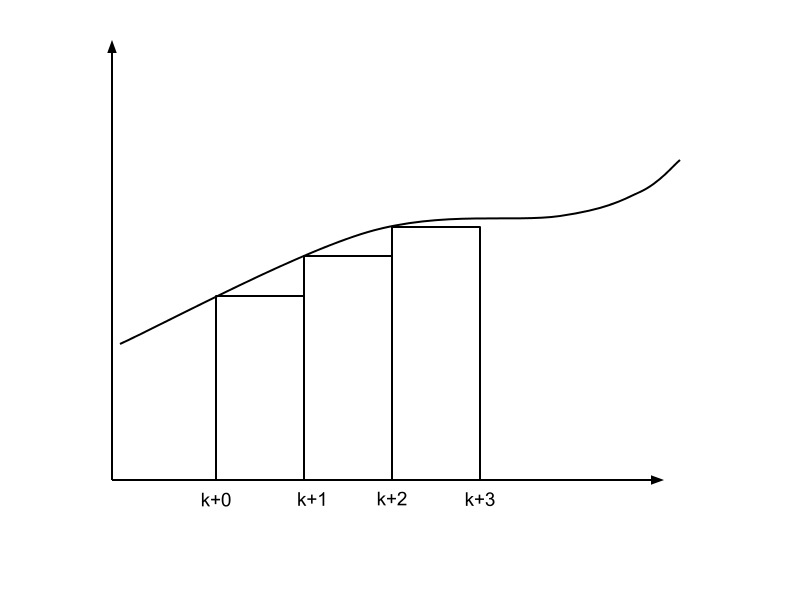
Für das erste Beispiel kann folgender Formelsatz (der einfachen LR-Kombination) entwickelt werden: \[ x_{k+1} = x_k + \Delta t \cdot f(x_k) = i_k + \Delta t \cdot \frac{E(t_k)-R \cdot i_k}{L} \]
Um die Schreibweise etwas zu vereinfachen, werden ein paar Hilfsvariablen eingeführt: \[i0 = i(t_k) \] \[ i1 = i(t_{k+1}) \] \[e0 = E(t_k) \] \[ e1 = E(t_{k+1}) \] Die Formel sieht dann etwas augenfreundlicher so aus: $$ i1 = i0 + \Delta t \cdot \frac{e0 - R \cdot i0}{L} $$ Jetzt kann man in der Programmiersprache seiner Wahl eine Schleife über die Formel laufen lassen, und damit den Zeitverlauf numerisch ermitteln.
Für das Beispiel mit der Matrixschreibweise wird das ganze jetzt etwas komplizierter. Aus der Ausgangsgleichung muss der Differentialqotient errechnet werden: $$ A_1 \cdot \dot{x} + B_1 \cdot x = C_1 \;\;\;\; \to \;\;\;\; \dot{x} = A_1^{-1} \cdot (C_1-B_1 \cdot x) $$ Oder etwas programmiererfreundlicher in der Zeitschrittform: $$ x1 = x0 + \Delta t \cdot A_1^{-1} \cdot (C_1-B_1 \cdot x0) $$
Hier fällt schon das erste Problem auf, daß die Matrix \( A_1 \) invertiert werden muss. Leider ist die Determinate der Matrix in diesem Beispiel \( 0 \), das geht schief! Ab hier muss man also in die Trickkiste greifen: z.b. Hinzufügen von hochohmige, parasitären Widerständen parallel zu den Induktivitäten. Die Matrix wird dadurch invertierbar, jedoch ist die Lösung mathematisch sehr instabil, da hinzugfügten Leitwerte sehr kleine Werte haben (müssen).
Generell wird beim expliziten Euler für den Zeitschritt der alte Zeitschritt ( also der Stromwert und auch der alte Spannungswert) verwendet. Dies ist möglich, da das Verfahren davon ausgeht, daß sich die Zustandsgrößen innerhalt des Zeitschrittes fast nicht (also nur sehr wenig) ändern. Dadurch hat das Verfahren allerdings auch massive numerische Probleme, die sehr kleine Schrittweiten erfordern. Diese kleinen Zeitschritte führen auch zu sehr kleinen Differenzen in den Zustandsgrößen und den Differenzialquotienten. Diese kleinen Änderungen in den Zustandsgrößen führen wiederum zu einem numerischen Integrationsproblem bei Gleitkommazahlen. Die Lösung tendiert dazu „wegzulaufen“ oder aufzuschwingen.