
Wer sich schon ein wenig mit Leistungselektronik und Umrichtern beschäftigt hat, hat sich irgendwann gefragt: Wie steuere ich die Zündimpulse meiner Leistungshalbleiter?
Die Frage wir hier teilweise geklärt. Teilweise deshalb, da hier nur auf da klassische Unterschwingungsverfahren eingangangen wird. Teilweise auch deshalb, weil nur klassische 2-Punkt-Umrichter betrachtet werden.
Die nachfolgen Kurven sind online berechnete Kurven. Hier kann, je nach Prozessorstärke und Browser, mit den Werten gespielt werden.
| Netzfrequenz: | Hz | |
| Netzspannung (LL eff): | V | |
| Drosselinduktivität: | mH | |
| Zwischenkreisspannung: | V | |
| Pulszahl: | - | |
| Halbe Abtastung?: | - | |
| Simulationsschrittweite: | us | |
| Minimalstrom für fft: | A |
Das Unterschwingungverfahren beruht darauf, dass zwei Kurven miteinander verglichen werden. Eine Stellgröße und eine Dreieckfunktion mit der Schaltfrequenz. Stellgröße ist hierbei die "Soll"sinusspannung.
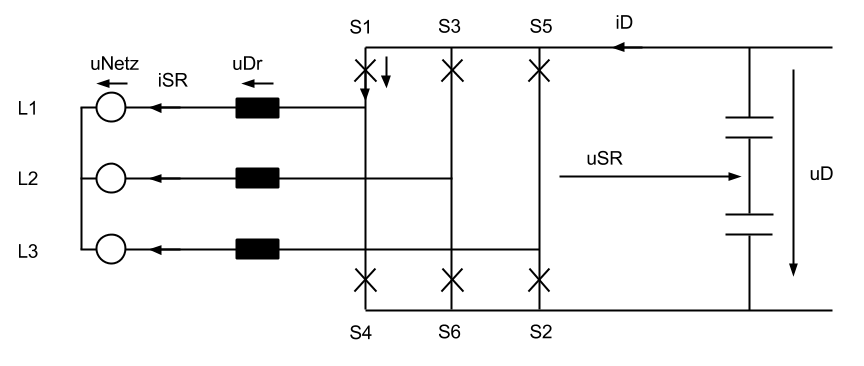
Die Schaltmuster sind so definiert, das bei positive Vorzeichen der jeweils obere Leistungshalbleiter "EIN" ist, bei negativem Vorzeichen der unterer Leistungshalbleiter "EIN" ist.
Es gibt zwei Schaltspannungen des Umrichters: Eine Spannung ist die Spannung gegen die Zwischenkreismitte, die andere
Spannung wird gegen einen virtuellen Trafosternpunkt definiert. Da bei praktisch alle dreiphasigen Umrichtern der Trafosternpunkt
nicht mit der Zwischenkreismitte verbunden ist, ist die resultierende Spannung über der Drossel NULLsystemfrei.
Nachfolgend wird die SR-Spannung gegen Zwischenkreismitte, die SR-Spannung gegen den virtuellen Trafosternpunkt sowie die Referenzspannung
dargestellt.
Die Spannungsdifferenz über der Drossel kann im Leerlauf mit der Spanungsdifferenz der (sinusförmigen)Sollspannung und der Umrichterausgangsspannung beschrieben werden, also der Spannungdifferenz aus obiger Grafik!
Um den oberschwingungsbehafteten Strom zu bekommen, muss die Spannung integriert werden: \( u_L= L \cdot \dot i_L -> i_L = \frac{1}{L} \cdot \int u_L dt \)
| Harmonische | Frequenz | i_abs/Arms |