Berechnung des Arbeitspunktes einer DAB

Worum gehts:


Die DAB benutzt eine Vollblocktaktung auf beiden Seiten. Diese beiden Blöcke können können unterschiedlich breit sein und gegeneinander verschoben sein. Dadurch können unterschiedliche AC-Spannungen am Trafo realisiert werden.
Die auf dieser Seite durchgeführt Arbeitspunktberechnung für eine DAB wird grundsätzlich über die Pulsverschiebung zwischen links und rechts gerechnet. Es kann auch eine Solleistungsvorgabe durchgeführt werden, jedoch wird diese Sollleistung wiederum über unterschieliche Phasenverschiebungen "ausprobiert".
Ein kritischer Punkt ist die "Null-Schaltzeit". Diese Zeit gibt an, wann zb die erste Brücke zuschaltet, nachdem die zweite abgeschaltet hat.Es handelt sich also um die Zeit, in der sowohl die linke, als auch die rechte Brücke einen Nullvektor fahren. Das ist dann gleichzeitig die Zeit vom "Nullstrom", also dem Magnetisierungsstrom des Trafos.
Bei Teillast kann diese Nullzeit erhöht werden um einen schöneren/besseren Stromverlauf zu bekommen. Dies wurde hier aber nicht implementiert.

Formelsatz:

Der erste Freiheitsgrad ist die Verschiebung der Blöcke (also links-rechts) zueinander. Dabei stellt sich eine unterschiedliche Wirkleistung in Abhängigkeit des Winkels über den Trafo ein. Bei einer Verschiebung von Null gibt es keine Wirkleistung. Die Phasenverschiebung sollte zwischen -30..30 Grad liegen. Je größer der Winkel bei Nennlast ist, umso mehr Streuung muss in den Trafo eingebaut werden. Dadurch steigt dann auch der Blindleistungsbedarf des Trafos und die AC-Ströme gehen bei Last überproportional hoch.
\( (1) \; phaseShift_{deg} = f(Wirkleistung) \)
An einem Trafo sollte die Primärspannung gleich der Sekundärspannung sein. Dies ist der zweite Freiheitsgrad. Dies führt dazu, daß der Trafo seine Grundschwingungsblindleistung von links und rechts gleichzeitig bekommt. Der Trafo bekommt also von links und rechts die gleichen Spannungs-Zeit-Flächen. Hier muss natürlich noch die Übersetzung des Trafos berücksichtigt werden. Die Aussteuerung der Vollbrücke ist zwischen 0..1 definiert.
\( (2)\; v_{AC.left} = v_{AC.right} \cdot trafo_{ratio} \)
\( (2)\; v_{DC.left} \cdot a_{left} = v_{DC.right} \cdot a_{right} \cdot trafo_{ratio} \)
Der dritte Freiheitsgrad betrachtet die Kurvenform selber. Es geht hier um die "Null-Schaltzeit" (tNullRef_pu) zwischen dem Schalten der Pulse. Es muss immer einen (kurzen) Moment geben, in der die Spannung am Trafo rechts und links gleichzeitig Null ist. Nur dadurch können die Brücken praktisch stromlos einschalten. Die Länge dieses Zeitraumes kann man in [pu] des Gesamtzeitraumes bemessen. Ein Wert von 0.02 [pu] == 2% erscheint gut. Die Nullzeit tritt zweimal pro Grundschwingung auf.
Das Kriterium der Nullschaltzeit führt automatisch bei einer hohen Phasenverschiebung == hohe Leistung zu geringen Aussteuerungen. Hierdurch würden die Aussteuerungen bei hohen Leistungen geringer sein, als bei geringen Leistungen. Dies erzeugt jedoch eine regelungsteschniche Nichtlinearität. Hier kann man dem mit entsprechenden Aussteuerbegrenzungen vorbeugen, die sich dann bei Teillast bemerkbar machen.
\( td_{pu} = \frac { | phaseShift_{deg} |} {90} \)
\( (3)\; a_{left} + a_{right} = 2 - 4 \cdot tNullRef_{pu} - td_{pu} \)
Die Nullschaltzeit berechnet sich dabei zu:
\( tNullAct_{pu} = \frac { 2 - td_{pu} -aLeft - aRight } {4} \)
Der vierte Freiheitsgrad betrachtet die Einschaltpulse der beiden Brücken. Hier darf dier verzögerte Brücke die erste Brücke nicht bei den Einschaltimpulsen überholen. Insbesondere im Leerlauf ( also bei einer Phasenverschiebung gleich null ) tritt dieser Fall sehr leicht auf. Daher ist eine negative Pulsdifferenz manchmal nicht zu verhindern.
\( td_{pu} = \frac { | phaseShift_{deg} |} {90} \)
(4) \( | a_{left} - a_{right} | = td_{pu} - 4 \cdot tPulsDiffRef_{pu} \)
Die Plusdifferenz berechnet sich dann zu:
\( tPulsDiffAct_{pu} = \frac { td_{pu} - | a_{left} - a_{right} | } {4} \)
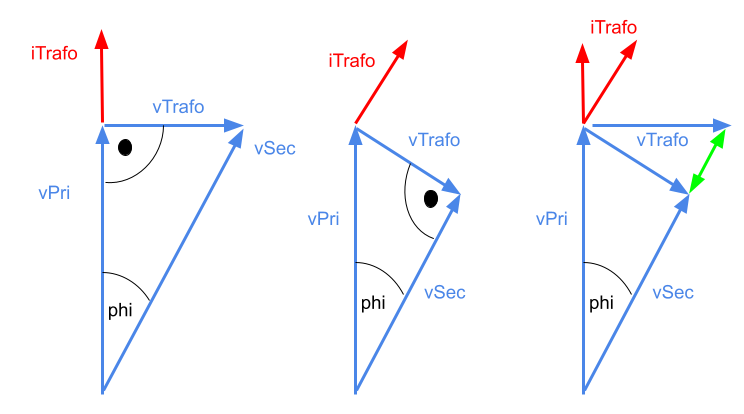
Der fünfte Freiheitsgrad betrachtet die Blindleistung der Brücken. Prinzipiell sollten die Brücken selber keine Blindleistung zueinander schieben. Die von den beiden Brücken in Summe produzierten Blindleistungen darf also nicht größer sein als die Blindleistungsaufnahme der Trafostreuung. Die beiden AC-Spannungen dürfen also nur soweit voneinander abweichen, dass die Blindleistung nur der Blindleistungsafnahme der Trafostreuung entspricht. Der grüne Bereich kennzeichnet hier den erlaubten Bereich.

\( v_L = vDc_{left} \)
\( v_R = vDc_{right} \cdot ue_{Trafo} \)
\( (5a) \; v_L \cdot a_{left} = v_R \cdot a_{right} \cdot \cos(\phi) \)
\( (5b) \; v_L \cdot a_{left} \cdot \cos(\phi) = v_R \cdot a_{right} \)
Durch (2) und (3) sind die Aussteuerungen der beiden Vollbrücken definiert. Es gibt jedoch Momente, vor allem bei Teillast oder bei starken Spannungsunsymmetrien, bei der die Pulse künstlich schmaler gemacht werden sollen. Um dies zu Erreichen kann die "Null-Schaltzeit" vergrößert werden. Hier bietet sich ein Lookup-Table an.

Berechnung der Aussteuerungen:

Im Prinzip ist die Phasenverschiebung der Brücken fix. Was übrig bleibt ist nur die Berechnung der beiden Aussteuerungen. Die Anzahl der Möglichkeiten ist also begrenzt.

Optimierungsziele

  • Prinzipiell sollte die Ausstuerung so hoch als möglich sein. Die ergibt sich automatisch aus der Leistungsbetrachtung, die sie aus der Multiplikation von Strom und Spannung berechnet. Für die gleiche Leistung brauche ich also deutlich mehr Strom, wenn die Spannung sinkt.
  • Es sollte auch möglichst keine Blindleistung von der Brücke links nach rechts ( oder Umgekehrt) transportiert werden. Dies erfordert einen zusätzlichen Blindstrom, der sich zu einem höheren Gesamtstrom addiert, und damit Zusatzverluste generiert.
    • Erster Schritt der Berechnung
    Hier werden die Aussteuerungen nach der Spannungslage definiert. Es gibt hier eine Fallunterscheidung, in Abhängigkeit davon, welche der beiden DC-Spannungen kleiner ist. Es wird immer mit den Spannungen bezogen auf die linke Brücke gerechet.
    \( vL = vDc_{left} \)
    \( vR = vDc_{right} \cdot ue_{Trafo} \)
    Die Spannung links ist größer als rechts: \( vL > vR \)
  • \( a_{Right} = a_{Max} \)
  • \( a_{Left} = a_{Max} \cdot \frac{vR}{vL} \)
    • Die Spannung links ist kleiner als rechts: \( vL < vR \)
  • \( a_{Left} = a_{Max} \)
  • \( a_{Right} = a_{Max} \cdot \frac{vL}{vR} \)
    • Am Ende der Berechnung müssen die Aussteuergrenzen überprüft werden.
    zweiter Schritt der Berechnung
    Jetzt muss grüft werden, ob die Nullschaltzeit verletzt wurde. Wurde diese verletzt, muss die Nullschaltzeit berücksichtigt werden.
    Wenn die errechnete Nullschaltzeit kleiner als die spezifizierte Nullschaltzeit ist, müssen die Aussteuerungen neu gerechnet werden.
    • \( k1 = tNullRef_{pu} \cdot 4 -2 + \frac { \lvert Phasenverschiebung \rvert } {90} \)
    • \( aLeft = -k1 \cdot \frac { vR } {vR + vL} \)
    • \( aRight = -k1 \cdot \frac { vL } {vR + vL} \)
    Auch hier müssen die Aussteuergrenzen geprüft werden.
    dritter Schritt der Berechnung
    Jetzt muss die Pulsdifferenz geprüft werden. Die Pulsdifferenz kann falsch sein, wenn es bei einer der Brücken zb. eine große Unterspannung gibt.
      Die Pulsdifferenzzeit berechnet sich dabei zu:
    • \( tD_{pu} = \frac { | Phasenverschiebung |} {90} \)
    • \( tPulsDiffAct_{pu} = \frac { tD_{pu} - | aLeft - aRight | } {4} \)
    Falls das Ergebnis kleiner als der erwartete Wert ist (zb 0) müssen die Aussteuerungen neu gerechnet werden. Dabei kann die Berechnung nach (2) und dieser (3) kombiniert werden.
    Über die Beziehung der Nullschaltzeit(3) und der Blindleistung(5) lassen sich auch Aussteuergrenzen berechnen. Hierbei ergeben sich dann Grenzen der Aussteuerungen, in den man sich bewegen darf.
      Die Aussteuerungen nach (3) und (5a) ergeben sich dann zu:
    • \( k1 = \frac{2 - 4 \cdot \frac{ t_{NullRef}}{tD_{pu} } } {v_R \cdot \cos(\phi) + v_L} \)
    • \( a_{right.max} = v_L \cdot k1 \)
    • \( a_{left.min} = v_R \cdot \cos(\phi) \cdot k1 \)
      Für den Formelsatz nach (3) und (5b) sieht es ähnlich aus:
    • \( k2 = \frac {2 - 4 \cdot \frac{ t_{NullRef}}{tD_{pu} } }{v_L \cdot \cos(\phi) + v_R} \)
    • \( a_{left.max} = v_R \cdot k2 \)
    • \( a_{right.min} = v_L \cdot \cos(\phi) \cdot k2 \)

    Steuersatz:

    Der Steuersatz ist bei Vollblocktaktung zwar einfach, bietet aber trotzdem Fallstricke. Hier hat muss die Vollblocktaktung symmetrisch erfolgen. Der IGBT/MOSFET der DAB schaltet bei (praktisch) Null Strom ein, und bei Nennstrom aus. Es fallen also nur Ausschaltverluste und Durchlassverluste an. Jetzt gibt es aber zwei Nullvektoren bei einer Vollbrücke:
    • beide Schalter oben ein
    • beide Schalter unten ein
    Die Ausschaltverluste treten immer dann auf, wenn in den Nullzustand "reingeschaltet" wird. Jetzt hat die DAB aber einmal positiven und einmal negativen Strom, wenn es zu diesem Abschaltvorgang kommt. Dadurch kommt es ( auf einen Schalter gesehen ) einmal zu einem echten Abschaltvorgang des IGBT/MOSFET und einem zu einem Abschaltvorgang der Diode. Der Abschaltvorgang der Diode macht aber nur sehr wenig Schaltverluste, so dass es zu einer Unsymmetrie der Schaltverluste kommt.
    Um dennoch die Schaltverluste auf alle 4 Schalter zu symmetrieren, muss ein Doppelzyklus (also zwei Zyklen) der DAB gerechnet werden. Die Nullvektoren müssen während dieses Doppelzyklus durchgetauscht werden. Es muss jede Transtition in beiden Richtungen durchlaufen werden.
    Zustandsreihenfolge der Schalter:

    (00)

    -

    (10)

    -

    (11)

    -

    (01)

    -

    (11)

    -

    (10)

    -

    (00)

    -

    (01)

    -

    (00)


    Verlustberechnung:


    Die Verlustberechnung berücksichtigt die Schalt- und Durchlassverluste der IGBT/MOSFET. Die Diode wird mit dem selben Vt0/Rx wie der IGBT/MOSFET gerechnet. Als Basis der Schaltverluste bei Diodenkommutierung dienen pauschal 5% der Schaltverluste des IGBT/MOSFET.

    Parameter

    Vordefinition:
    Modul links (click):
    Modul rechts (click):
    Leistung: kW
    Verschiebung: Grad
    Spannung DC, links: V
    Spannung DC, rechts: V
    Nennfrequenz: Hz
    minimale Aussteuerung: -
    maximale Aussteuerung: -
    Übersetzungsverhältnis links/rechts: -
    Trafostreuung, Summe, bezogen nach links: uH
    TrafoHauptind, bezogen nach links: uH
    Null-Schaltzeit, tNullRef_pu: pu
    tNullAct_pu
    tPulsDiffAct_pu
    links rechts
    Aussteuerung
    rms AC-Strom [A]
    max AC-Strom [A]
    rms AC-Spannung [V]
    Scheinleistung [kVA]
    dcCur, mean [A]
    iCZk, rms [A]
    losses IGBT [W] cond/swOn/swOff
    iOff IGBT [A]
    temp IGBT [K]
    losses bridge [kW]

    AC-Spannungen:
    Leistungen:
    AC-Ströme:
    DC-Ströme:
    Zündimpulse linke Brücke:
    Strom über Schalter linke Brücke:
    Verluste linke Brücke ( alle 4 Schalter ):
    Zündimpulse rechte Brücke:
    Strom über Schalter rechte Brücke:
    Verluste rechte Brücke ( alle 4 Schalter ):