ASM, T-Ersatzschaltbild, dq-mech-rotororientiert, in pu
Allgemeines
Das T-Ersatzschaltbild kommt der Physik der Asynchronaschine am nächsten. Es wird hierbei mit drei Induktivitäten entsprechend der Flüsse gearbeitet:
- Ständerstreuinduktivität, die Feldlienien, die aus dem Ständer kommen, durch den Luftspalt gehen, und wieder in den Ständer zurückgehen
- Hauptinduktivität, die Feldlinien, die Ständer zu Läufer und wieder zurück gehen
- Läuferstreuinduktivität, die Feldlienien, die aus dem Läufer kommen, durch den Luftspalt gehen, und wieder in den Läufer zurückgehen
Aus diesen drei Teilflüssen können wiederum 3 Flussverkettungen gebaut werden:
- Ständerfluss = Ständerstreufluss + Hauptfluss
- Hauptfluss , siehe Hauptinduktivität
- Läuferfluss = Läuferstreufluss + Hauptfluss
Alle diese drei Flüsse sind fast gleich groß und unterscheiden sich vor allem in der Orientierung.
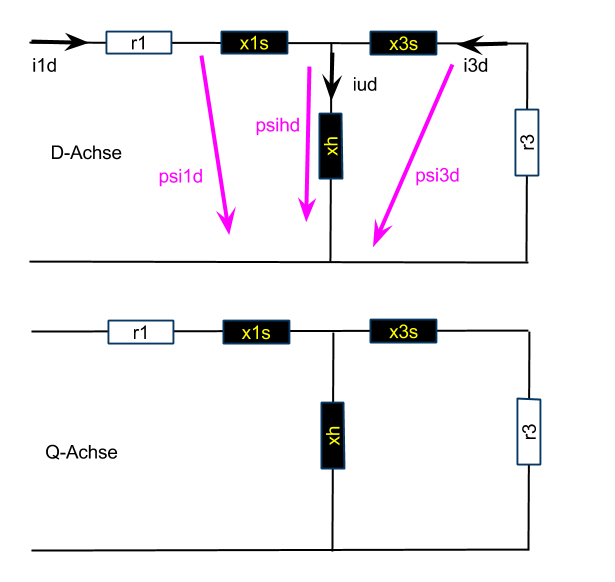
Simscape Modell
Formelsatz
Die Gleichungen arbeiten alle "pu". Typische Werte:
- r1 (Ständerwiderstand) : 0.01 … 0.05
- xs1 (Ständerstreuung) : 0.03 … 0.15
- xh (Hauptinduktivität) : 2 .. 3
- r3 (Läuferwiderstand) : 0.02 … 0.1
- xs3 (Läuferstreuung) : 0.03 … 0.1
Die Orientierung des Modells ist mechanisch-rotororientiert. Vorstellung:
- Man öffnet den Motor.
- Man zieht den Rotor raus
- jetzt malt man auf den Rotor mit Kreide jeweil ein D, Q, -D , -Q drauf und verteilt das ganze gleichmäßig über dem Umfang. Falls die Maschine 4-polig ist (eine Netzmaschine mit 1400 U/min Nenndrehzahl ist 4 polig), dann muss man das entsprechend doppelt machen. Also: D, Q,-D, -Q,D,Q,-D,-Q.
- Man klebt auf das erste D und Q jeweils einen Magnetfeldsensor. Es gibt also nur zwei Sensoren!
- dieSensoren werden irgendwie :-) verkabelt, der Rotor kommt zurück in den Ständer
- diese beiden Sensoren messen dann den Läuferstreufluss \( {\Psi}3_d \) und \( {\Psi}3_q \)
- falls man die Sensoren nicht direkt auf den Läufer klebt, sondern noch 1mm Beilage drunterpackt, erhält man den Hauptfluss \( {\Psi}h_d \) und \( {\Psi}h_q \)
- den Ständerstreufluss \( {\Psi}1_d \) und \( {\Psi}1_q \) mit der Methode zu messen wird etwas schwierig, da der Sensor dann magnetisch mit dem Ständer verbunden sein müsste, sich aber mechanisch mit dem Rotor mitdrehen muss.
Ständergleichungen:
- \( U1_d = r1 \cdot i1_d + \frac{ d{\Psi}1_d }{\omega_n \cdot dt} - n \cdot {\Psi}1_q \)
- \( U1_q = r1 \cdot i1_q + \frac{ d{\Psi}1_q }{\omega_n \cdot dt} + n \cdot {\Psi}1_d \)
Läufergleichungen:
da es sich um einen Kurschlussläufer handelt, sind die Spannungen 0.
- \( 0 = r3 \cdot i3_d + \frac{ d{\Psi}3_d }{\omega_n \cdot dt} \)
- \( 0 = r3 \cdot i3_q + \frac{ d{\Psi}3_q }{\omega_n \cdot dt} \)
Flussgleichungen:
Ständerfluss
- \( {\Psi}1_d = x{\sigma}1 \cdot i1_d + {\Psi}h_d \)
- \( {\Psi}1_q = x{\sigma}1 \cdot i1_q + {\Psi}h_q \)
Läuferfluss
- \( {\Psi}3_d = x{\sigma}3 \cdot i3_d + {\Psi}h_d \)
- \( {\Psi}3_q = x{\sigma}3 \cdot i3_q + {\Psi}h_q \)
Hauptfluss
- \( {\Psi}h_d = xh \cdot i{\mu}_d \)
- \( {\Psi}h_q = xh \cdot i{\mu}_q \)
Stromsummen:
- \( i1_d + i3_d = i{\mu}_d \)
- \( i1_q + i3_q = i{\mu}_q \)
Drehmoment:
Das Drehoment ist: M = Im{psi*conj(I)}
- \( M_{el} = {\Psi}h_d \cdot i1_q - {\Psi}h_q \cdot i1_d \)
Drehwinkel:
Der Drehwinkel ist der Orientierungswinkel, auf den die Achsen D und Q bezogen sind
- \( \frac{d\rho}{\omega_n \cdot dt} = n \)
Drehzahl:
- \( \frac{dn}{dt} = \frac{M_{el}-M_{Last}}{ {\tau}_J} \)
Realisierung in einer Programmiersprache
Der Gleichungssatz wurde mit Javascript implementiert.
Der Ausgangspunkt bildet hier ein Unterprogramm, dem eine Struktur mit den von Zeitschritt zu Zeitschritt zu übertragenden Zustandsgrößen, also den Strömen und den Flüssen.
Die Netzspannung in Ständerkoordinaten:
Die Ströme in Ständerkoordinaten:
Die Ströme zeigen ein kurzes Einschwingen. Da der Motor mit Nennlast betrieben wird,
sind die Strangströme (i1_ab) praktisch in Phase zur Netzspannung, da der Magnetisierungsstrom
nicht weiter auffällt.
Die Spannungen und Flüsse in Rotorkoordinaten:
Die Flüsse der ASM werden mit dem Schlupf der Maschine mitgedreht. Der Fluss
hat die Ständerfrequenz, "hinkt" aber 90Grad nach. Auf das
Läuferkoordinatensystem bezogen (also das Bezugssystem dieses Formelsatzes)
hat der Fluss die Schlupffrequenz.
Die Ströme in Rotorkoordinaten:
Sowohl für die Ständer- als auch für die Läuferströme gilt: da das Bezugssystem
die Rotormechnik ist, ist die resultierende Frequenz die Schlupfrequenz

